Seispalabras: ¿Truco o trato? ¿Capirotes o triángulos?

Como dicen en mi tierra algunas personas mayores, que un carnaval coincida con la celebración de la semana santa cristiana, debe ser un contraDios... pero así ha sido. En cualquier caso, es un carnaval de matemáticas, nada carnal, me temo. Yo me alegro porque siendo semana santa tengo más tiempo libre para muchas cosas. Entre otras, para escribir esta entrada y para playear :)

Durante esta semana, al menos en mi comunidad autónoma, los niños tienen descanso desde el lunes posterior al Domingo de Ramos al viernes llamado santo (para mí serían santos todos. Menos el último de agosto, eso sí).

Pues pensando en ellos, en los niños, y no sólo en ellos, os propongo unos juegos con triangulaciones de puntos para jugar con ellos, con sólo un papel y un par de bolígrafos de 2 colores, por si no os gusta ir de capirotes...

Por ejemplo, en un restaurante en el que tarden en serviros, le dais la vuelta al mantelito de papel de los niños y usáis los lapicitos de colores. Si es un restaurante más elegante, siempre podéis pedir papel.

Antes que nada, vamos a explicar que es una triangulación de un conjunto de puntos. Si tenemos un conjunto P de puntos dibujados en el plano, una triangulación de dicho conjunto P es una conjunto maximal de segmentos uniendo por parejas a puntos de P, es decir, ponemos segmentos entre cada pareja de puntos, mientras no se corten entre ellos.

Vamos a verlo gráficamente. Supongamos que el conjunto de puntos P es el que aparece en la siguiente figura

Ahora vamos a triangular dicho conjunto de puntos, añadiendo, mientras podamos, es decir, mientras no corte a segmentos ya existentes, segmentos uniendo puntos de P, de dos en dos. Por ejemplo, la siguiente figura, ¿muestra una triangulación de P?

Evidentemente, no, porque aún podemos añadir un segmento más en el cuadrilátero sombreado en amarillo en la figura siguiente.

Y la siguiente figura, ¿muestra una triangulación de P?

Pues tampoco, puesto que hay dos segmentos que se cortan en el cuadrilátero sombreado en verde de la figura siguiente:

Esto que viene a continuación sí sería una posible triangulación de P

Ahora todos sabemos que es una triangulación.

Cuando mis hijos eran pequeños, hasta aquí llegaba el juego. Las tardes de lluvia y frío que no podíamos salir a potrear al parque y que se me ponían una “mijita” nerviosos, yo pintaba puntos en un papel y les retaba a que los triangulasen, porque me ayudarían con mi trabajo. Así descubrí, por ejemplo, que cuando habían hecho 4 ó 5 triangulaciones distintas, al empezar la siguiente, lo primero que dibujaban era la frontera de la envolvente convexa de P, demostrando, al menos para mí, que se trata éste, el concepto de envolvente, de un concepto intuitivo, puesto que ellos no lo conocían, pero lo intuyeron.

Además vamos a definir un tipo de transformación en la triangulación, estos es, vamos a dar un método para transformarla en otra. En inglés, se le llama Diagonal Flip y en español, casi todos los que la usamos le llamamos simplemente Flip e incluso conjugamos el verbo flipar al usar dichas transformaciones. Sólo en grupos reducidos de trabajo, claros, no en artículos de investigación, ésos están escritos en inglés.

Si elegimos un segmento (arista) interno de la triangulación, de los que no están “por fuera” (en la envolvente convexa), dicho segmento será la unión de dos triángulos que, unidos, definen un cuadrilátero. Pues bien, “flipar” el segmento interno, es intercambiarlo, cuando sea posible, por la otra diagonal del citado cuadrilátero.

Como dicen que una imagen vale más que no sé cuántas palabras...

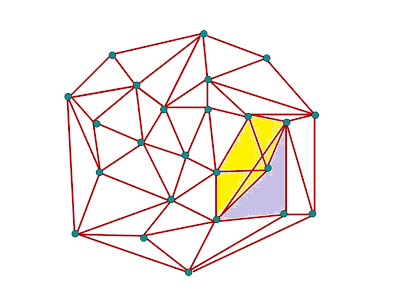
Pero, ¿se pueden flipar (intercambiar) todos las aristas internas de una triangulación y que siga siendo una triangulación válida? La respuesta es no, como se puede deducir de la siguiente figura:

Si flipamos la diagonal de cuadrilátero sombreado, no sería ya una triangulación, porque cortaría a otras aristas de la misma y dejaría un cuadrilátero, el morado, vamos un desastre...

Pues ahora ya sí, sabemos lo que es una triangulación de un conjuntos de puntos y como “flipar” las aristas internas de dicha triangulación.

Describamos los juegos. Los clasificamos en dos tipos:

Juegos de Construcción
Juegos de Transformación o de “flipe”

Podéis jugar también en la playa y molesta menos que las paletas :)

Juegos de Contrucción de triangulaciones.

Para estos juegos, sólo tenemos que pintar de entrada el conjunto de puntos

Triangulación (2 jugadores, 1 hoja de papel y un lápiz)

En este juego, se trata de construir una triangulación de P. Cada jugador dibuja una arista en cada turno. Cada vez que un jugador complete 1 o más triangulos , se los apunta a su cuenta y tiene turno extra. Al terminar la triangulación, gana quién más triángulos tenga.

Por ejemplo, si dibujamos estos puntos en nuestro papel

Y elegimos a un contrincante (jugador 2) no demasiado despierto, (esto simplemente para que sea más corto para mí ilustrar elejmplo) , sería algo así

Cazar el triángulo (2 jugadores, 1 hoja de papel y un lápiz)

Es exactamente como el juego anterior, pero gana el primero que termine un triángulo.

Triangulación bicromática (2 jugadores, 1 hoja de papel y 2 lápices de distinto color)

Es como el primer juego descrito, el de la triangulación, pero ahora cada jugador tiene un color asignado y sólo se anotarán los triángulos monocromáticos, es decir, con las tres aristas del mismo color, de su color, claro está.

Cazar al triangulo monocromático (2 jugadores, 1 hoja de papel y 2 lápices de distinto color)

Es igual que el anterior, pero gana el primero que consiga terminar un triángulo con las tres aristas de su color.

Juegos de Tranformación de triangulaciones o de “flipe”

Aquí, de entrada, necesitamos un triangulación de puntos ya dibujada, supongamos que en negro, ¿vale?

Flipando (2 jugadores, 1 hoja de papel, un lápiz verde)

Cada jugador, por turno, elige una arista NEGRA interna de la triangulación, si la puede flipar, la flipa y la dibuja en verde, la nueva arista. Gana el que haga el último flip posible. Las aristas verdes no se pueden volver a flipar.

Flipando y al triángulo cazando (2 jugadores, 1 hoja de papel, un lápiz verde)

Es como el anterior, pero el ganador es el primero que complete un triángulo verde, con las tres aristas verdes.

Flipando en colores (2 jugadores, 1 hoja de papel, dos lápices de distinto color)

Es como los dos anteriores, pero cada vez que un jugador flipa una arista NEGRA, colorea con su color la nueva arista y las que sean negras en el cuadrilátero definido por la arista flipada, con su color. El juego acaba cuando no se pueden seguir flipando aristas internas negras y gana el que haya dibujado más aristas en su color. Igual que antes, sólo se pueden flipar las aristas que sean todavía NEGRAS.

Ha jugado el ROJO

El jugador AZUL elige cuadrilátero donde flipar

Sólo pinta de AZUL las aristas del cuadrilátero que eran NEGRAS.

Y eso es todo, amigos, por ahora... Estoy segura de que os gustará intentar alguno de estos juegos.

Todos estos juegos y alguno más están descritos en este trabajo. Hace no muchos días, buscando material para mi asignatura de Geometría Computacional, optativa en el plan de Ingeniería Informática, me topé con este trabajo. En el mismo trabajo se analiza la conexión de algunos de estos juegos con triangulaciones con otros juegos tales como Kayles. Así mismo, los autores presentan algunas estrategias ganadoras para algunos de los juegos de triangulaciones cuando los puntos están distribuidos en algunas posiciones concretas (posición convexa)

Aparte de entretener a niños y mayores con este tipo de juegos, las triangulaciones tienen una infinidad de aplicaciones muy interesantes en áreas muy diversas. Ya se mencionó en este mismo blog la aplicación de las mismas en el problema de la galería de arte y lo importante que son para mí desde un punto de vista profesional y también personal. Pero hay muchas más. Seguiremos informando.

Para terminar este post, quiero agradecer la colaboración a SuperTriángulo (@SuperTriangulo)